Comparison of algorithms
In this table,
n is the number of records to be sorted. The
columns "Average" and "Worst" give the time complexity in each case,
under the assumption that the length of each key is constant, and that
therefore all comparisons, swaps, and other needed operations can
proceed in constant time. "Memory" denotes the amount of auxiliary
storage needed beyond that used by the list itself, under the same
assumption. These are all
comparison sorts.
The run time and the memory of algorithms could be measured using
various notations like theta, omega, Big-O, small-o, etc. The memory and
the run times below are applicable for all the 5 notations.
The following table describes
integer sorting algorithms and other sorting algorithms that are not
comparison sorts. As such, they are not limited by a

lower bound. Complexities below are in terms of
n, the number of items to be sorted,
k, the size of each key, and
d,
the digit size used by the implementation. Many of them are based on
the assumption that the key size is large enough that all entries have
unique key values, and hence that
n << 2
k, where << means "much less than."
Non-comparison sorts
| Pigeonhole sort |
— |
 |
 |
 |
Yes |
Yes |
|
| Bucket sort (uniform keys) |
— |
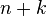 |
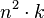 |
 |
Yes |
No |
Assumes uniform distribution of elements from the domain in the array.[2] |
| Bucket sort (integer keys) |
— |
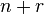 |
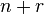 |
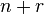 |
Yes |
Yes |
r is the range of numbers to be sorted. If r =  then Avg RT = then Avg RT =  [3] [3] |
| Counting sort |
— |
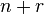 |
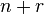 |
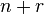 |
Yes |
Yes |
r is the range of numbers to be sorted. If r =  then Avg RT = then Avg RT =  [2] [2] |
| LSD Radix Sort |
— |
 |
 |
 |
Yes |
No |
[3][2] |
| MSD Radix Sort |
— |
 |
 |
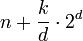 |
Yes |
No |
Stable version uses an external array of size n to hold all of the bins |
| MSD Radix Sort |
— |
 |
 |
 |
No |
No |
In-Place. k / d recursion levels, 2d for count array |
| Spreadsort |
— |
 |
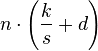 |
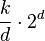 |
No |
No |
Asymptotics are based on the assumption that n << 2k, but the algorithm does not require this. |
The following table describes some sorting algorithms that are
impractical for real-life use due to extremely poor performance or a
requirement for specialized hardware.
Additionally, theoretical computer scientists have detailed other sorting algorithms that provide better than

time complexity with additional constraints, including:
- Han's algorithm, a deterministic algorithm for sorting keys from a domain of finite size, taking
 time and
time and  space.[4]
space.[4]
- Thorup's algorithm, a randomized algorithm for sorting keys from a domain of finite size, taking
 time and
time and  space.[5]
space.[5]
- An integer sorting algorithm taking
 expected time and
expected time and  space
space
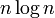
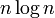

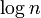
















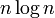
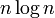
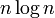
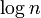








 comparisons when the data is already sorted or reverse sorted.
comparisons when the data is already sorted or reverse sorted.


















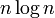





 comparisons when the data is already sorted, and 0 swaps.
comparisons when the data is already sorted, and 0 swaps.



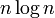
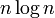





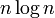








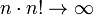


 lower bound. Complexities below are in terms of n, the number of items to be sorted, k, the size of each key, and d,
the digit size used by the implementation. Many of them are based on
the assumption that the key size is large enough that all entries have
unique key values, and hence that n << 2k, where << means "much less than."
lower bound. Complexities below are in terms of n, the number of items to be sorted, k, the size of each key, and d,
the digit size used by the implementation. Many of them are based on
the assumption that the key size is large enough that all entries have
unique key values, and hence that n << 2k, where << means "much less than."


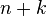
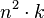

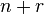
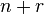
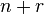
 then Avg RT =
then Avg RT =  [3]
[3]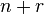
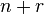
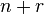
 then Avg RT =
then Avg RT =  [2]
[2]




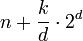




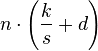
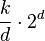







 parallel processors. Spaghetti sort#Analysis
parallel processors. Spaghetti sort#Analysis


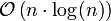
 time complexity with additional constraints, including:
time complexity with additional constraints, including: time and
time and  expected time and
expected time and
No comments:
Post a Comment